Образование: теория и практика » Проектирование уроков по теме "Площади плоских фигур" » Планы-конспекты уроков

Планы-конспекты уроков

Страница 9

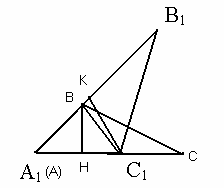
Рис. 34.

Перемножая полученные равенства, находим:

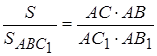или .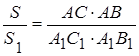

Теорема доказана.

4. Закрепление изученного материала (6 мин)

Решить устно задачи:

1.Дано: . Найти .

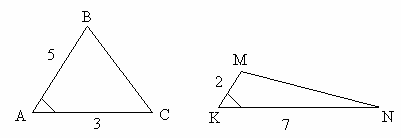
Рис. 35.

2. Дано: ОА=8 см, ОВ=6 см, ОС=5 см, OD=2 см, см2. Найти .

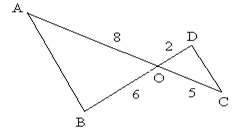
Рис. 36.

Решить самостоятельно задачу:

Площадь одного равностороннего треугольника в 3 раза больше, чем

площадь другого равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1.

Решить самостоятельно задачу № 479 б).

5. Самостоятельная работа обучающего характера (10 мин)

I уровень

I вариант

1. Две стороны треугольника равны 12 см и 9 см, а угол между ними

300. Найдите площадь треугольника.

2. Дано: АО=4, ВО=9, СО=5, DO=8, SAOC=15. Найти SBOD.

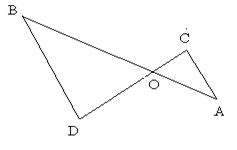
Рис. 37.

II вариант

1. Найти площадь треугольника, две стороны которого равны 6 см и 8 см, а угол между ними 300.

2. Дано: АО=10, ВО=8, СО=12, DO=8, SВOD=14. Найти SAOC.

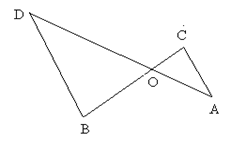
Рис. 38.

II уровень

I вариант

1. В треугольнике ABC , ВС=10 см, а высота ВD делит сторону АС на отрезки AD=6 см, DC=8 см. Найдите площадь треугольника и высоту,

проведенную к стороне ВС.

2. Дано: ВО=АО, ОС=2OD, SAOC=12 см2. Найдите SBOD.

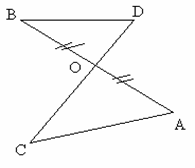
Рис. 39.

II вариант

1. В треугольнике ABC , AB=10 см, а высота AD делит сторону CB на отрезки DB=6 см, DC=8 см. Найдите площадь треугольника и высоту, проведенную к стороне AВ.

2. Дано: ВО=CО, ОD=3OA, SAOC=16 см2. Найдите SBOD.

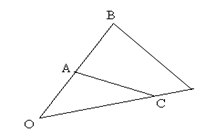
Рис. 40.

III уровень

I вариант

1. В треугольнике АВС , , АВ=10 см. Найдите площадь треугольника.

2. Дано: ОА=АВ, АС || BD. Доказать, что SOBC=SOAD.

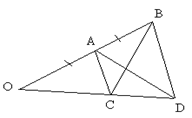
Рис. 41.

II вариант

1. В треугольнике АВС . Найдите ВС, если площадь треугольника равна 36 см2.

2. Дано: ВС=АВ, ВЕAD, CDAD. Доказать, что SACD=4SABE.

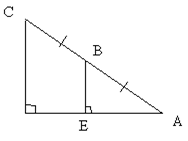
Рис. 42.

6. Домашнее задание (3 мин)

П. 52, вопрос 6.

I уровень

Решить задачи № 479 а), 476 а);

II уровень

Решить задачи № 479 а), 476 а), 477;

III уровень

Решить задачи № 479 а), 476 а), 477;

Дополнительная задача: Дан четырехугольник ABCD, О – точка пересечения его диагоналей. АО=3 см, ВО=6 см, OD=4 см, SAOC+SBOD=39 см2. Найдите SAOC.

Страницы: 4 5 6 7 8 9 10 11 12 13 14

Материалы по педагогике:

Методологические особенности проектной деятельности детской школы искусств
Социокультурное проектирование - это специфическая технология, способ достижения определённого результата. Это конструктивная, творческая деятельность, сущность которой заключается в анализе проблем и выявлении причин их возникновения, выработке целей и задач, характеризующих желаемое состояние объ ...

Исследование по выявлению проблем профессионального становления студентов из числа детей-сирот
Исследование проводилось на базе Поморского государственного университета им. М.В. Ломоносова, факультета педагогики начального образования и социальной педагогики в марте-апреле 2011 года. Основан в 1932 г. В структуре университета 21 факультет, 66 кафедр, 27 научных центров и лабораторий; филиалы ...

Особенности социально-педагогической поддержки профессионального становления студентов из числа детей-сирот
Адаптация детей-сирот в вузе - это сложный многоуровневый процесс приспособления и утверждения личности в новых для нее условиях социальной среды на стадии самостоятельного жизнеустройства. Процесс адаптации в этот период времени направлен на формирование позитивной жизненной установки сироты в соц ...

Планы-конспекты уроков

Разделы