Образование: теория и практика » Проектирование уроков по теме "Площади плоских фигур" » Планы-конспекты уроков

Планы-конспекты уроков

Страница 5

2. ABCD и DCMK – квадраты. AB=6 см. Найдите площадь и периметр четырехугольника OCPD.

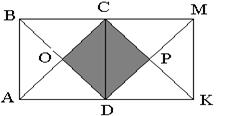
Рис. 18.

III уровень

I вариант

1. В трапеции ABCD A=450, С=1000. Диагональ BD составляет с боковой стороной CD угол 350. На стороне AB построен параллелограмм ABPK так, что точка D принадлежит отрезку BP и BD:DP=2:1. Найдите площадь параллелограмма, если его периметр равен 30 см.

2. ABCD – прямоугольник; M, P, K, T – середины его сторон, AB=6 см, AD=12см. Найдите площадь четырехугольника MPKT.

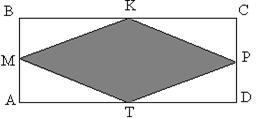
Рис. 19.

II вариант

1. В трапеции MPKOM=450, K=1350. На стороне MP трапеции построен параллелограмм MPDT так, что его сторона PD параллельна прямой KO и пересекает сторону MO в точке A, причем PA:AD=1:3. Площадь параллелограмма равна 36 см2. Найдите его периметр.

2. ABCD – прямоугольник; M, P, K, T – середины его сторон, AB=16 см, AD=10см. Найдите площадь шестиугольника AMKCPT.

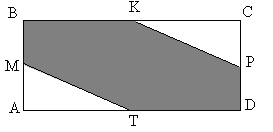
Рис. 20.

6. Домашнее задание (2 мин)

П.50, вопрос 3.

Дополнительная задача: Дан прямоугольник ABCD, его периметр равен 44 см, DC:AD=7:4, DE=FC=EF/2, где точки Е и F лежат на стороне DC. Найти площадь треугольника АВК.

6. Подведение итогов урока (1 мин)

Площадь прямоугольника равна произведению его смежных сторон.

Урок № 3

Тема: Площадь параллелограмма

Цели урока:

1. Образовательная: учащиеся должны знать формулу для вычисления

площади параллелограмма, уметь вывести эту формулу. Выработать у учащихся умение применять полученные знания в решении задач.

2. Развивающая: развивать логическое, абстрактное мышление, быстроту внимания; формировать приемы умственной деятельности: сравнения, аналогии, сопоставления; углублять и систематизировать знания по данной теме; развивать точную, лаконичную речь.

3. Воспитательная: учить преодолевать трудности; работать в быстром темпе, собираться с мыслями и принимать решение; воспитывать стремление к совершенствованию знаний.

Ход урока

1. Организационный момент (2 мин)

Учитель приветствует учащихся, сообщает тему урока, его цели, проводит проверку присутствующих.

2. Актуализация знаний учащихся (10 мин)

Теоретический опрос

а) Сформулируйте основные свойства площадей многоугольников.

б) Назовите признаки равенства прямоугольных треугольников.

в) Сформулируйте и докажите теорему о площади прямоугольника (один ученик готовится у доски, в это время остальные проверяют домашнее задание).

Проверка домашнего задания

Проверить решение домашних задач (учитель выборочно проверяет тетради учащихся).

Решение задач с целью подготовки учащихся к восприятию нового материала

1. Дано: ABCD – параллелограмм, BM=4, MN=6, BMAD, CNAD. Доказать, что SABM=SDCN. Найти SABCD.

2. Дано: ABCD – параллелограмм, ВКAD, BAD=450, ВК=6. Найти SABCD.

3.Изучение нового материала (10 мин)

Перед выводом формулы площади параллелограмма следует ввести понятие основания и высоты параллелограмма. НА доске и в тетрадях – рисунок. BH – высота, проведенная к стороне AD параллелограмма ABCD. BK – высота, проведенная к стороне CD параллелограмма ABCD.

Страницы: 1 2 3 4 5 6 7 8 9 10

Материалы по педагогике:

Чтение познавательной природоведческой художественной литературы о природе
Знакомя детей с природой, мы должны не только сообщать им конкретные знания, но и вызывать в душе каждого ребёнка эмоциональный отклик, пробуждать эстетические чувства. Каждый объект природы, яркий или скромный, большой или маленький, по своему привлекателен, и, описывая его, ребёнок учиться опреде ...

Метод круговой тренировки на уроках в 5-9-х классах
Раздел "Легкая атлетика". В 5-9-х классах уроки выстраиваются с учетом возрастных особенностей. К 14-15 годам несколько снижается эффективность скоростных и скоростно-силовых упражнений, т.к. в этом возрасте снижается прирост быстроты. На уроках легкой атлетики, для развития скоростных ка ...

Кружковая работа с природным материалом как форма и метод развития творческих способностей детей с особыми образовательными потребностями
Надежда Константиновна Крупская в одной из своих работ обращала внимание на то, что «…Надо сделать так, чтобы труд был и интересный и посильный, и в то же время, чтобы это был творческий труд, а не только механический». Полученные на уроке труда умения и навыки в работе с природным материалом и инс ...

Планы-конспекты уроков

Разделы