Образование: теория и практика » Проектирование уроков по теме "Площади плоских фигур" » Планы-конспекты уроков

Планы-конспекты уроков

Страница 4

3) Т.к. AK=CK, то KAC =KCA как углы при основании равнобедренного треугольника AKC.

AKC= 1200, тогда KAC =KCA=300. https://pro-ekip.ru мужская мотозащита купить.

4) BCD=900, BCA=300, тогда DCA=600.

Ответ: 300, 600.

в) Выполнить практические задания (устно):

1. Докажите, что два прямоугольника равны, если равны их смежные стороны.

2. На рисунке 14 ABCD — квадрат, MN||AB, EF||BC. Найдите площадь четырехугольника AFKM, если AM=CE=3 см, DE = 6 см.

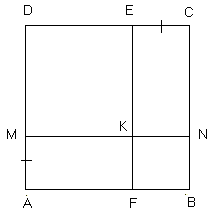
Рис. 14.

3. Объяснение нового материала (8 мин)

Вспомнить с учащимися, что ранее уже встречались с формулой для вычисления площади прямоугольника. Поэтому логично задать следующий вопрос: как вычислить площадь прямоугольника. Ученики могут ответить по-разному: а умножить на b, длину умножить на ширину. Следует подсказать, что длина и ширина прямоугольника есть его смежные стороны. Таким образом, будет сформулирована следующая теорема, которую учитель доказывает у доски:

Теорема. Площадь прямоугольника равна произведению его смежных сторон.

Доказательство. Рассмотрим прямоугольник со сторонами a, b и площадью S. Докажем, что S = ab.

Рис. 15.

Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке 16.

По свойству 30 площадь этого квадрата равна (a + b)2.

Рис. 16.

С другой стороны, этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S (свойство 10 площадей) и двух квадратов с площадями a2 и b2 (свойство 30 площадей). По свойству 20 имеем:

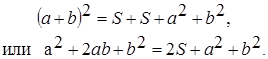
Отсюда получаем S = ab.

Теорема доказана.

4. Закрепление изученного материала (10 мин)

Решить устно задачи № 452 а), в), 453 в).

Решить на доске и в тетрадях задачу

I уровень: № 454;

II уровень: № 455, 456;

III уровень: № 457, 458.

Решить в тетрадях задачу № 501 самостоятельно.

5. Самостоятельная работа обучающего характера (7 мин)

I уровень

I вариант

1. Найдите площадь прямоугольника, если его периметр равен 80 см, а отношение сторон равно 2:3.

2. Площадь пятиугольника AOBCD равна 48 см2. Найдите площадь и периметр квадрата ABCD,если О – точка пересечения диагоналей квадрата.

II вариант

1. Найдите периметр прямоугольника, если его площадь равна 98 см2, а

1. Найдите периметр прямоугольника, если его площадь равна 98 см2, а одна из его сторон вдвое больше другой.

2. Периметр квадрата ABCD равен 48 см. Найдите площадь пятиугольника ABOCD, где О – точка пересечения диагоналей квадрата.

II уровень

I вариант

1. В прямоугольнике ABCD сторона AD равна 10 см. Расстояние от точки пересечения диагоналей до этой стороны равно 3 см. Найдите площадь прямоугольника.

2. ABCD и MDKP – равные квадраты. AB=8 см. Найдите площадь и периметр четырехугольника ACKM.

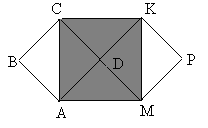
Рис.17.

II вариант

1. Площадь квадрата равна 36 см2. Найдите расстояние от точки пересечения диагоналей квадрата до его сторон.

Страницы: 1 2 3 4 5 6 7 8 9

Материалы по педагогике:

Семинар как форма активизации познавательной деятельности
Видовые методы занятий носят целенаправленный характер и соответствуют определенным видам занятий, большинство из них включают семинары. Семинар - это: • «вид учебных занятий, обсуждение учащимися под руководством преподавателя подготовленных ими сообщений и докладов»; • «форма учебного процесса, п ...

Использование малых форм фольклора в ознакомление с природой и формировании экологических знаний
Пословицы, поговорки, загадки, небольшие стихи предлагаются детям в процессе наблюдения. Образный язык их помогает выделить особенности явления, определенные качества предмета, усилить эстетическое восприятие природы. Во время наблюдения зимой за льдом, снегом, погодой воспитатель загадывает загадк ...

Школа как координатор совместной деятельности школы и семьи
В ходе изложения теоретических и методических основ обучения и воспитания неоднократно подчеркивалось, что их успешное осуществление происходит только при условии объединения воспитательных усилий школы, семьи и общественности. Не следует забывать, что влияние семьи на развитие и формирование детей ...

Планы-конспекты уроков

Разделы