Образование: теория и практика » Проектирование уроков по теме "Площади плоских фигур" » Планы-конспекты уроков

Планы-конспекты уроков

Страница 7

3. Изучение нового материала (10 мин)

Задача

В треугольнике ABC AB=c, CH – высота, CH=h. Найти SABС.

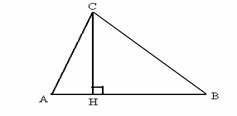
Рис. 24.

Учащиеся решают задачу самостоятельно, после обсуждения решения

задачи в тетрадях и на доске записывается:

, ,

где a – сторона треугольника, ha – высота, проведенная к стороне a.

Затем учитель формулирует следствия из этой теоремы.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.

Следствие 2. Если высоты двух треугольников равны, то их площади относятся как основания.

Доказательства данных утверждений учащиеся разбирают самостоятельно по учебнику.

4. Закрепление изученного материала (17 мин)

Решить устно задачи № 468 а), б), 471, 474. К задаче № 474 на доске или на плакате заранее подготовить рисунок.

Решить на доске и в тетрадях задачу

I уровень: № 470;

II уровень: № 472;

III уровень: № 473, 474.

Решить самостоятельно задачи № 472, 475.

6.Домашнее задание (2 мин)

П. 52, вопрос 5.

I уровень

Решить задачи № 468 в), г), 473;

II уровень

Решить задачи № 468 в), г), 473, 469;

III уровень

Решить задачи № 468 в), г), 473, 469;

Дополнительная задача: В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, которая удалена от прямой CD на 4 см. Найдите площадь треугольника АОВ, если CD=8 см.

7. Подведение итогов урока (1 мин)

Площадь треугольника равна половине произведения его основания на высоту.

Урок № 5

Тема: Площадь треугольника. Решение задач

Цели урока:

1. Образовательная: рассмотреть теорему об отношении площадей треугольников, имеющих по равному углу, совершенствовать навыки решения задач.

2. Развивающая: развивать логическое, абстрактное мышление, быстроту внимания; формировать приемы умственной деятельности: сравнения,

аналогии, сопоставления; углублять и систематизировать знания по данной теме; развивать точную, лаконичную речь.

3. Воспитательная: учить преодолевать трудности; работать в быстром

темпе, собираться с мыслями и принимать решение; воспитывать стремление к совершенствованию знаний.

Ход урока

1. Организационный момент (2 мин)

Учитель приветствует учащихся, сообщает тему урока, его цели, проводит проверку присутствующих.

2. Актуализация знаний учащихся (10 мин)

Теоретический опрос (подготовиться у доски)

- Сформулируйте и докажите теорему о площади треугольника. (Один ученик II или III уровня готовит доказательство теоремы у доски.)

- Выведите формулу для вычисления площади прямоугольного треугольника. (Один ученик II или III уровня готовит доказательство теоремы у доски.)

- Докажите, что если высоты треугольников равны, то их площади

относятся как основания. (Один ученик II или III уровня готовит доказательство теоремы у доски.)

Решение задач (письменно с последующей проверкой)

I уровень

1. Найти SABC. (Ответ: 36 кв. ед.)

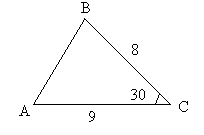
Рис. 25.

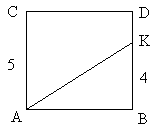
2. На рисунке 26 ABCD – квадрат, AB=5 см, KB=4 см. Найти SABCK. (Ответ: 15 см2)

3. На рисунке 27 АВС – треугольник. Найти SABC. (Ответ: 120 см2)

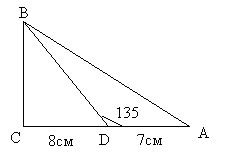
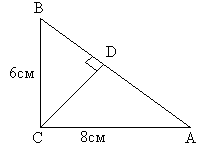
4. На рисунке 28 АВС – треугольник, угол С – прямой, AB=10. Найти

CD. (Ответ: 4,8 см)

Страницы: 2 3 4 5 6 7 8 9 10 11 12

Материалы по педагогике:

Языковое тестирование как способ контроля при обучении английскому языку
Одним из наиболее эффективных средств контроля в обучении ИЯ считается тест. В зарубежной литературе по тестированию под педагогическим или психологическим тестом часто понимают процедуру, предназначенную для выявления конкретного образца поведения (в нашем случае – речевого), из которого можно сде ...

Анализ и обобщение результатов опытно-экспериментальной работы
В период обобщающего этапа опытно-экспериментальной работы (2004 – 2005 учебный год) в музыкально-ритмические занятия были включены все виды деятельности, которые мы рассмотрели, а также уделялось особое внимание формированию интонационной выразительности речи как условия развития творческого потен ...

Характеристика структуры опытно-экспериментальной работы и её основных элементов
Важным условием оптимизации учебного процесса является систематическое получение учителем объективной информации о ходе усвоения знаний учащимися, которую учитель получает в процессе контроля учебно-познавательной деятельности учащихся Контроль означает выявление, установление и оценивание знаний у ...

Планы-конспекты уроков

Разделы