Образование: теория и практика » Анализ ошибок заочной математической школы » Сравнение и аналогия

Сравнение и аналогия

Страница 1

Сравнение – это установление сходства или различия между предметами или их отдельными признаками . Сравнение приводит к правильному выводу, если выполняются следующие условия: сравниваемые понятия однородны и сравнение осуществляется по таким признакам, которые имеют существенное значение. Смотрите подробности курс в обменниках екатеринбурга здесь.

Процесс сравнения и аналогия тесно связаны. Можно сказать, что сравнение подготавливает почву для применения аналогии. С помощью аналогии сходство предметов, выявленное в результате их сравнения, распространяется на новое свойство. Рассуждения по аналогии можно представить следующей схемой:

Объект A обладает свойствами c1, c2, …, cn.

Объект B обладает свойствами c1, c2, …, cn-1.

Предполагается, но не утверждается, что B обладает свойством cn. Именно поэтому аналогию нельзя считать доказательным методом, ее еще надо обосновать. Тем не менее, рассуждения по аналогии полезны в процессе обучения, так как подразумевают самостоятельную формулировку новых теоретических фактов. Основная ошибка школьников при применении аналогии – это отсутствие рассуждений, которые бы полностью ее обосновывали. Без них решение является неполным или просто неверным.

Рассмотрим наиболее часто встречающиеся в решениях школьников виды необоснованных аналогий:

1) Расширение сферы применения теоремы. Появление такого рода ошибки, как правило, связано с формальным знанием теоремы или свойства. В сознании ученика четко не выделены условия применимости теоремы, и в результате некоторые из них остаются за пределом его рассмотрения. Следствием этого является незаконное использование теоремы. По сути ученик применяет не теорему, а ее аналог, который нередко оказывается неверным. Рассмотрим пример:

Пример Aн1: Хорда, не проходящая через центр окружности, равна диаметру.

Доказательство: Дана окружность с диаметром AB. Выберем на ней произвольно точку C. Середина AC – точка D. Проведем через точки B и D хорду BE.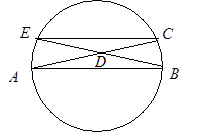 Теперь соединим точки C и E.

Рассмотрим треугольники ADB и DCE. Они равны по стороне и двум углам: AD = DC по построению; ÐB = ÐC как вписанные, опирающиеся на одну дугу AE; ÐADB = ÐCDE как вертикальные. Значит соответствующие стороны AB и EC равны.

Анализ ошибки: «Равенство треугольников по стороне и двум углам» – именно такую условную формулировку часто дают признаку равенства треугольников по стороне и прилежащим к ней углам. В результате школьники просто ищут пары равных элементов: AD = DC, ÐB = ÐC, ÐADB = ÐCDE. При этом условие, что углы должны быть прилежащими соответственно к сторонам AB и DC, забывается. Буквальное восприятие условной формулировки признака равенства треугольников приводит к замене его совсем другим. Произошло расширение сферы применения признака. Ученик воспользовался им без выполнения надлежащих условий, он заменил их на более общие. Это и привело к противоречивому факту – равенству хорды, не проходящей через центр, диаметру. В этом случае лучше всего будет, если ученик самостоятельно, просмотрев предварительно точную формулировку признака равенства треугольников, найдет у себя ошибку.

2) Использование вместо теоремы обратного к ней утверждения. Смысл рассуждений при этом заключается в следующем: если у нас верно AÞB, то верным будет и BÞA. Понятно, что это выполняется не всегда. Приведем простой пример, когда обратная теорема не верна, и ее применение приводит к противоречивому результату.

Пример Ан2: Докажем, что все числа равны.

Для этого возьмем два произвольных числа a и b. Докажем, что a = b.

0 = 0 Þ a2 – 2ab +b2 = b2 –2ab + a2 Þ (a – b)2 = (b – a)2 Þ a – b =

= b – a Þ 2a = 2b Þ a = b.

Переход (a – b)2 = (b – a)2 Þ a – b = b – a не верен. Дело в том, что из равенства чисел следует равенство их квадратов, но из равенства квадратов не следует равенство чисел (будут равны лишь их модули).

3) Ошибки при попытке обобщения. Пусть у нас имеется класс A и класс B. Для элементов класса A выполняется свойство CA. Делается предположение, что для элементов класса B будет выполняться условие CB, которое построено по аналогии со свойством CA в соответствии с особенностями класса B. Например:

Страницы: 1 2

Материалы по педагогике:

Модельное занятие №2 Использование инновационных образовательных технологий в учебном процессе: проблемы и перспективы
1. Прочтите текст одного кейса (на выбор), проявите, какие образовательные технологии используют педагоги при организации учебного процесса 2. Чем, по вашему мнению, обоснован выбор преподавателем той, или иной технологии 3. В чём специфика, характерные особенности технологий, используемых преподав ...

Европейские стандарты и руководящие принципы Болонского процесса в свете Интернет-экзамена ФЭПО
В мае 2005 года разработаны так называемые Европейские стандарты и руководства для систем гарантии качества высшего образования, которые утверждены советом министров европейских стран, отвечающих за образование. Один из руководящих принципов звучит так: в вузах должны разрабатываться системы, помог ...

Понятие методологии и ее сущность
Не только педагоги-практики, нередко за понятием “методология” видят нечто абстрактное, далекое от реальной жизни и от образовательной практики. Между тем методология – это система принципов и способов организации и построения теоретической и практической деятельности.1 Есть и другие определения ме ...

Сравнение и аналогия

Разделы