Образование: теория и практика » Организация процесса повторения в курсе геометрии 7-9 классов » Подготовка учителя к урокам повторения

Подготовка учителя к урокам повторения

Страница 5

Но функции упражнений при повторении этим не исчерпываются. При выполнении упражнений требуется что-то большее, чем простое запоминание данных. Эти данные должны быть «схвачены» как единое целое с пониманием взаимной зависимости каждой части от остального.

Таким образом, при выполнении упражнений происходит более глубокое осмысливание теории и совершенствуется навык в ее приложении к различным объектам.

В процессе повторения необходимо подбирать задачи, не входящие в стабильный учебник, с помощью которых иллюстрируются свойства рассматриваемых фигур и соотношения между ними. Когда же курс планиметрии окончен и выделяется несколько уроков на повторение, целесообразно подобрать серию задач не только наиболее полно затрагивающих теорию, но и выводящих учащихся на новый, более качественный виток. При этом развитию интереса к геометрии способствует связь между предложенными задачами по теме или методу решения. Активность детей еще более усилится, если предложить им находить в этих задачах связи между фигурами или их элементами. При этом не только происходит систематизация знаний, но и возникает желание импровизировать, составлять новые задачи, самостоятельно находить обобщения и связи фигур.

Все это говорит о том, что повторение нельзя вести в отрыве от упражнений, ибо при изучении наук, как справедливо утверждал Исаак Ньютон, примеры не менее поучительны, чем правила .

Например, на уроке повторения по теме «Четырехугольники» можно использовать такую систему задач:

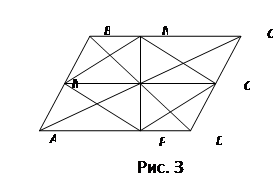Решение комплексной задачи. Прежде чем предъявлять учащимся задачу, которая требует довольно сложного чертежа, учитель дает классу ряд простых задач на построение, из которых постепенно складывается чертеж: постройте параллелограмм ABCD; постройте его диагонали, обозначьте точку их пересечения через О; постройте прямую, проходящую через точку О и пересекающую сторону AD в точке Р, а сторону ВС — в точке N; постройте прямую, проходящую через точку О и пересекающую сторону АВ в точке М, а сторону CD — в точке Q. В конце этих построений учащиеся получают чертеж, как на рис. 3. По этому чертежу предлагается следующая задача:

Дан параллелограмм ABCD. Через точку пересечения его диагоналей проведены две прямые, пересекающие стороны АВ и CD, ВС и AD соответственно в точках М и Q, N и Р. Докажите, что четырехугольник MNQP — параллелограмм.

Решение нестандартных задач практического характера:

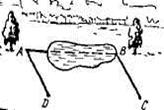
Как на местности измерить расстояние между точками A и В, используя свойство сторон параллелограмма (рис. 4 )?

Достаточно ли для проверки того, что данный четырехугольный кусок материи имеет форму ромба, проверить совпадение краев при сгибании его по каждой диагонали?

Пользуясь только линейкой с параллельными краями, проведите перпендикуляр к отрезку через его середину (длина отрезка больше ширины линейки).

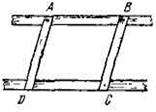
Объясните устройство приспособления для вычерчивания параллельных прямых (рис. 5).

Обычно такие задания вызывают у учащихся интерес к геометрии, развивают наблюдательность, смекалку.

Недооценка роли упражнений при повторении, равно как и ее переоценка, неизменно приводит к формализму в знаниях теории, к снижению образовательного уровня учащихся.

В школе ни одно понятие или учение нельзя довести до полного понимания без системы хорошо подобранных упражнений.

Отсюда не следует, что все повторение нужно заменить только упражнениями. Упражнения, являясь составной частью повторения, тем не менее, не могут заменить само повторение.

Для закрепления усвоенных учащимися теоретических знаний следует в большей степени использовать решение различного рода задач.

Каждая задача представляет собой исключительно важное по своему значению и разностороннему охвату средство повторения теории, закрепления основных положений этой теории и усовершенствования учебных навыков. Особенно это заметно сказывается, когда основные этапы решения задачи и производимые в них преобразования обосновываются. В задачах и упражнениях ученик встречает вопросы теории в новых связях, в новых сочетаниях, в несколько перестроенном виде, и ученику приходится пользоваться этой теорией применительно к условиям решаемой задачи. Усилия ученика в этом направлении способствуют устранению формализма в его знаниях.

Страницы: 1 2 3 4 5 6 7 8 9 10

Материалы по педагогике:

Школа искусств как институт развития детского музыкального творчества
В решении поставленных государственных задач воспитания и образования детей и молодежи важная роль отведена системе детских школ искусств, в деятельности которых определяющей функцией является развитие склонностей, способностей, интересов, социального и профессионального самоопределения детей и под ...

Понятие методологии и ее сущность
Не только педагоги-практики, нередко за понятием “методология” видят нечто абстрактное, далекое от реальной жизни и от образовательной практики. Между тем методология – это система принципов и способов организации и построения теоретической и практической деятельности.1 Есть и другие определения ме ...

Образование как процесс
Образование как процесс отражает этапы и специфику развития образовательной системы как изменение ее состояния за конкретный временной период. Эта динамическая характеристика образования связана с процессом достижении цели, способами получения результата, затраченными при этом усилиями, условиями и ...

Подготовка учителя к урокам повторения

Разделы