Образование: теория и практика » Организация процесса повторения в курсе геометрии 7-9 классов » Подготовка учителя к урокам повторения

Подготовка учителя к урокам повторения

Страница 6

Использование задач, систематизированных определенным образом – это один из путей повышения эффективности процесса повторения. Так как в большинстве своем геометрические задачи менее алгоритмичны, чем алгебраические, то особое значение приобретает обучение учащихся общим приемам решения задач. Поэтому повторению подлежат не только определения и теоремы, но и общие приемы решения задач, логические конструкции, геометрические конфигурации.

Большой дидактической целью обладают задачи, в которых требуется найти свойства и отношения реализуемые на некоторой конфигурации. На удачно подобранной конфигурации можно повторить многие вопросы курса геометрии. Но главное, что на таких примерах учащиеся обучаются планомерному, комплексному анализу чертежа, у них формируется и развивается «геометрическое видение», оттачивается интуиция.

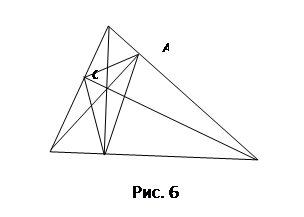Например: «В треугольнике АВС проедены высоты , , . Точки , , , последовательно соединены (рис. 6). Найдите свойства и отношения которые выполняются на данной конфигурации».

Эта конфигурация дает богатый материал для повторения вопросов «Углы в треугольнике», «Подобие», «Площади подобных фигур». Добавив описанную окружность, получаем вписанные углы и т.д.

Работая с конфигурацией, учащиеся могут открыть «свои» теоремы, например: «Высоты треугольника содержат биссектрисы треугольника ».

При работе с такими задачами можно использовать следующую методику. Учащимся на дом предлагается задание – найти свойства и отношения, реализуемые на данной конфигурации, а затем, используя найденные свойства, составить свои задачи. Эти задачи могут быть либо обсуждены на очередном уроке со всем классом, либо предложены для самостоятельного решения в классе. Происходит своего рода математическое соревнование – кто больше всего придумал «своих» задач и больше решит «чужих».

Уроки-упражнения, особенно при повторении, — трудные уроки. Здесь учитель должен учесть фактор времени и вместе с тем повторить основное содержание темы. Это требует, чтобы на повторение выносилась продуманная система упражнений, которая обеспечивала бы глубокое и всестороннее осмысливание учебного материала.

Очень полезно также, особенно в конце года, когда повторяется весь материал, рекомендовать учащимся отыскать решения одних и тех же задач различными способами. Иногда этого можно достигнуть различными вариациями чертежа к задаче. Сначала учитель сам предлагает задачу и к ней чертеж в различных вариациях, а затем требует оформить решение задачи, исходя из предложенного чертежа.

Например, задача. «Определить площадь трапеции, у которой основания равны 60 см и 20 см, а боковые стороны — 13 см и 37 см».

Решить задачу, составляя уравнение, исходя из чертежей (рис. 7).

Рис. 7

Учащиеся приспосабливают решение задачи к чертежу, у них выступают в различных сочетаниях те или иные положения пройденного ранее материала, при этом не всегда одни и те же положения служат основой (идеей) решения данной задачи. Следовательно, рассмотрев в классе, а затем, проанализировав дома решение какой-нибудь задачи на различных чертежах, учащиеся за короткий срок повторяют значительный материал из пройденного.

Но такая работа положительна и в другом отношении Учащиеся на подобных примерах видят, что на практике требуется непосредственное измерение на местности, выбор данных очень часто диктуется условиями местности, а потому приходится готовить данные сообразно этим условиям.

На опыте такого разнообразия решения задач мы поставили перед учащимися вопрос о сравнительной оценке каждого способа решения, степени его соответствия критерию экономии сил, изящества и простоты, одним словом предложили дать оценку качества решения.

Страницы: 1 2 3 4 5 6 7 8 9 10

Материалы по педагогике:

Экскурсия - форма воспитания экологического сознания и эстетического мировосприятия
Тема опыта: "Экскурсия – форма воспитания экологического воспитания и эстетического мировосприятия". Сведения об авторе. Условия возникновения опыта. Актуальность опыта. На основе разработки научных представлений и обобщения передового опыта сложилась характеристика эстетического воспитан ...

Педагогическая теория Аристотеля
Будучи учеником Платона, Аристотель рано, однако, разошелся во взглядах со своим учителем, не принял его учения о разделении мира на мир идей и мир вещей. Оставшись на позициях объективного идеализма, он разработал ряд материалистических положений. Аристотель признавал единство мира, неотделимость ...

Анализ использования активных методов обучения в подготовке специалистов дошкольного образовании в педагогическом колледже
В процессе прохождения государственной практики в ГОУСПО "Алексеевском педагогическом колледже" нами была проведена опытно-экспериментальная работа. Экспериментальное исследование включало три этапа: констатирующий, формирующий, контрольный. Опытно-экспериментальная работа проводилась с э ...

Подготовка учителя к урокам повторения

Разделы