Образование: теория и практика » Проектирование уроков по теме "Площади плоских фигур" » Планы-конспекты уроков

Планы-конспекты уроков

Страница 19

Ход урока

1. Организационный момент (2 мин)

Учитель приветствует учащихся, сообщает тему урока, его цели, проводит проверку присутствующих.

2. Актуализация знаний учащихся (6 мин)

Теоретический опрос

Выведите формулу площади правильного многоугольника (один ученик готовит ответ у доски).

Проверка домашнего задания

Проверить решение задач.

3. Объяснение нового материала (17 мин)

Сначала необходимо напомнить учащимся определение площади произвольной фигуры и дать определение понятия «круг». Затем учитель выводит формулу площади круга в соответствии с текстом учебника.

а) Кругом называется часть плоскости, ограниченная окружностью. Круг радиуса R с центром О содержит точку О и все точки плоски, находящиеся от точки О на расстоянии R.

б) Выведем формулу для вычисления площади круга радиуса R. Для этого рассмотрим правильный n – угольник А2А2…Аn, вписанный в окружность, ограничивающую круг. Очевидно, площадь S данного круга больше площади Sn многоугольника А2А2…Аn, так как этот многоугольник целиком содержится в данном круге. С другой стороны, площадь Sn’ круга, вписанного в многоугольник, меньше Sn, так как этот круг целиком содержится в многоугольнике. Итак, .

Будем теперь неограниченно увеличить число сторон многоугольника. Имеем 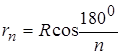, где rn – радиус вписанной в многоугольник окружности. При 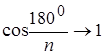, поэтому . Иными словами, при неограниченном увеличении числа сторон многоугольника вписанная в него окружность «стремится» к описанной окружности, поэтому при . Отсюда следует, что при .

Используя формулу для вычисления площади правильного многоугольника , где Рn –периметр многоугольника А2А2…Аn. Учитывая, что при , получаем:

Итак, для вычисления площади S круга радиуса R мы получим формулу .

4. Закрепление изученного материала (13 мин)

Решить на доске и в тетрадях задачи:

I уровень: 1116, 1117

II уровень: 1124, 1125

III уровень: 1126, 1127

5. Подведение итогов (2 мин)

Домашнее задание

Выучить п.111.

I уровень

Решить задачи №№ 1114, 1115;

II уровень

Решить задачи №№ 1114, 1115,1118;

III уровень

Решить задачи №№ 1114, 1115,1118;

Дополнительная задача: Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 см и 24 см.

Урок № 3

Тема: Площадь кругового сектора.

Цели урока:

1. Образовательная: учащиеся должны знать формулу для вычисления площади кругового сектора и уметь ее доказывать. Выработать у учащихся умение применять полученные знания в решении задач.

2. Развивающая: развивать логическое, абстрактное мышление, быстроту внимания; формировать приемы умственной деятельности: сравнения, аналогии, сопоставления; углублять и систематизировать знания по данной теме; развивать точную, лаконичную речь.

Страницы: 14 15 16 17 18 19 20 21 22

Материалы по педагогике:

Современные технологии воспитания
1. Опишите содержание этапов (алгоритмов) традиционной технологии воспитательной работы: 1-й этап (анализ исходных данных) – должен быть направлен на выяснение состояния основных компонентов воспитательного процесса: воспитанников, воспитателей (педагогов) и характер сложившихся между ними отношени ...

Роль музыкально-ритмических занятий в формировании интонационной выразительности речи в школе слабослышащих
Трудно не согласиться с мнением одного из педагогов современности, занимающегося обучением неслышащих детей И.С. Белик, «конечно же, музыка нужна любому человеку. Она развивает интонацию речи, слух, голос, темп, дыхание, память. Пластику движений, чувства, творческий потенциал. При том не только те ...

Краткий экскурс в историю "личностной компоненты" образования в отечественной педагогике
История российского образования содержательно связана с идеей человека в ее философско-религиозном истолковании. Именно на этой почве уже в конце XIX - начале XX веков (мы не касаемся более ранних дней, поскольку работа не носит собственно историографического характера) в России получили определенн ...

Планы-конспекты уроков

Разделы