Образование: теория и практика » Анализ ошибок заочной математической школы » Ошибки школьников ВЗМШ и их анализ

Ошибки школьников ВЗМШ и их анализ

Страница 1

Эта часть основана на конкретных работах учащихся ВЗМШ. Здесь мы выделили типичные ошибки, которые допускаются школьниками при выполнении заданий по пособиям, входящих в программу 8 класса Кировского отделения ВЗМШ. Анализ причины и соответствующие комментарии по ее исправлению, приведенные ниже по каждой из задач, могут быть использованы проверяющими при рецензировании работ учащихся. Кроме того, анализ причин основан на классификации ошибок, которая нами уже рассмотрена в §1. На ее основе мы и будем составлять соответствующие комментарии по задачам. Номера всех задач совпадают с их номерами в пособиях, которые приложены к настоящей работе.

Комбинаторика. Задания №1, №2.

Задача 1-7. AÈB содержит 25 элементов, AÇB – 10 элементов, B содержит 15 элементов. Найти количество элементов в A.

Рассуждения ученика: Так как множество B содержит 15 элементов, то множество A будет содержать 25 – 15 = 10 элементов.

Анализ ошибки: Следует заметить, что, выполняя задание “Комбинаторика”, большинство учеников впервые знакомятся с теорией множеств. В связи с этим они пытаются найти свойства, схожие со свойствами уже знакомых им объектов. Так операцию объединения двух множеств школьники часто связывают с операцией сложения двух чисел. Это вполне логично, ведь в свою очередь числа еще в младшем возрасте они изучали при помощи подручных предметов, к примеру, тех же счетных палочек, то есть, фактически, с помощью операций над множествами. При решении задачи ученик действовал с множествами, как с числами. Это было бы верно, если бы пересечение множеств было пустым, как при работе со счетными палочками. Но если это не так, то число элементов в объединении и сумма количеств элементов в каждом из множеств – это разные величины. Но ученик действовал по уже сформированному стереотипу, поэтому в ответе он получил не количество элементов множества A, а количество элементов, принадлежащих только A. Исходя из классификации, данной в §1, эту ошибку следует отнести к классу необоснованных аналогий. Причина ошибки состоит в том, что ребенок при решении задачи неосознанно работает с любыми двумя множествами как с непересекающимися. Проверяющему следует помочь ученику разобраться в понятиях пересечения и объединения, сделав упор на том, что отличает объединение множеств от сложения чисел. Это можно сделать, разобрав конкретную задачу. Целесообразно использовать круги Эйлера, так как графические иллюстрации помогают ученику лучше воспринимать информацию. Рассмотрим конкретный пример.

Задача. Множество A содержит 7 элементов, множество B – 10, объединение множеств A и B – 15.Сколько элементов содержит пересечение множеств A и B(c)?

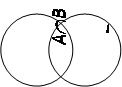Объединение множеств A и B можно разделить на три подмножества: 1) элементы, принадлежащие только множеству A; 2) элементы, принадлежащие пересечению множеств A и B; 3) элементы, принадлежащие только множеству B. Сложив количество элементов трех групп, мы получим количество элементов в объединении множеств A и B. Это видно и на кругах Эйлера. Обозначим за x – количество элементов пересечения. Тогда в первой группе 7 – x элементов, во второй x, в третьей 10 – x . В объединении (7 – x) + x + (10 – x) = 17 – x = 15 Þ x = 2. Можно предложить ученику решить данную задачу в общем виде, заменив числа 7, 10 и 15 на a, b и с. Тем самым он получит выражение с = a + b – х, характеризующее количественное отношение двух множеств.

Задача 1-14. Записать формулами множества, заштрихованные на диаграммах (приведено несколько диаграмм, из которых мы рассмотрим одну).

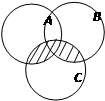Рассуждения ученика: Интересующее нас множество можно записать как AÇC + BÇC.

Анализ ошибки: Ученик отождествляет сложение с объединением. Надо убедить его, что между этими двумя операциями есть разница.

Не так важно, как называет ученик объединение (“объединение первого и второго множеств” или “прибавим к первому второе множество”, как-то иначе), важно то, что он подразумевает под ним, понимает ли он суть операции объединения. Поэтому нельзя считать, что ученик действовал при решении данной задачи неправильно. Надо указать, что при оперировании с числами употребляется знак “+”, а с множествами – “È”. Разделение этих операций исключает из рассуждений ненужную путаницу.

Страницы: 1 2 3 4 5 6

Материалы по педагогике:

Влияние семьи как социального института на формирование личности ребенка
Среди множества современных социальных институтов семья занимает одно из первых мест. Ее первостепенное влияние на ребенка нельзя отрицать, так как она закладывает фундамент будущей общественной жизни ребенка. Семья – это одна из ветвей воспитания подрастающего поколения, вторая – общественное. Сег ...

Функции и основные направления деятельности детских учреждений культуры
Понятие «социально-культурный институт» в самом широком смысле относится к любому из государственных, образований (центров, комплексов, одно- или многопрофильных организаций, учреждений и т. п.), обладающих социальной значимостью, целенаправленностью, организованной структурой, достаточной временно ...

Анализ использования активных методов обучения в подготовке специалистов дошкольного образовании в педагогическом колледже
В процессе прохождения государственной практики в ГОУСПО "Алексеевском педагогическом колледже" нами была проведена опытно-экспериментальная работа. Экспериментальное исследование включало три этапа: констатирующий, формирующий, контрольный. Опытно-экспериментальная работа проводилась с э ...

Ошибки школьников ВЗМШ и их анализ

Разделы