Опыт разработки объемных визуализаций по курсу физики

Наличие спина ядра i приводит к новой добавки энергии, обусловленной взаимодействием соответствующего магнитного диполя с суммарным магнитным полем движущегося в пространстве и обладающего спиновым моментом электрона. Учет указанного взаимодействия приводит к поправке следующего порядка малости, учет которой может быть проиллюстрирован в виде медленной прецессии векторов полного момента электрона и спина ядра вокруг их сохраняющейся во времени суммы f = j + i.

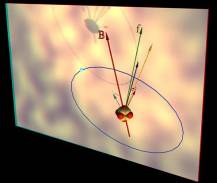
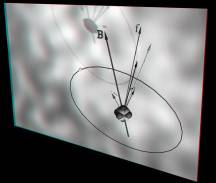
Рис.9. Векторная схема для помещенного во внешнее магнитное поле одноэлектронного атома, рассчитываемого с учетом тонкого и сверхтонкого расщепления уровней

При помещении атома во внешнее магнитное поле к описанному движению векторов добавляется прецессия полного момента f вокруг направлении, задаваемого вектором магнитной индукции В. Описанная система иерархий движения весьма сложна для восприятия, что делает оправданной попытку объемной визуализации ее временного поведения (рис. 9).

Заведомо более сложные векторные схемы возникают в случае многоэлектронных атомов, для которых векторы орбитального, спинового моментов электрона и спина ядра должны заменяться на аналогичные суммарные по всем электронам и нуклонам моменты, окруженные вращающимися вокруг них слагаемыми, соответствующими моментам каждой из частиц.

Практика по созданию объемных 3D проекций четырехмерных изображений была начата с разработки «тестовых» демонстраций четырехмерных аналогов стандартных геометрических примитивов: четырехмерных тетраэдра и куба (рис. 10).

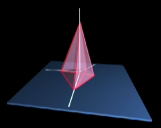
Рис.10. Стандартная 2D-проекция четырехмерного тетраэдра на плоскость и его объемная 3D-проекция на трехмерное пространство

Приведенные «тестовые» примеры ориентированы на решения важной задачи знакомства обучаемых с принятыми правилами построения объемных 3D проекций объектов из четырехмерного евклидового пространства. Следующим шагом является переход к 3D отображению четырехмерного пространства-времени Минковского. Простейшим объектом такого пространства является световой конус, регистрируемый наблюдателем, покоящимся относительно расположенного в начале координат источником света. Традиционное изображение светового конуса на плоскости и варианты анаглифической визуализации его проекции в трехмерное пространство приведены на рис.11.

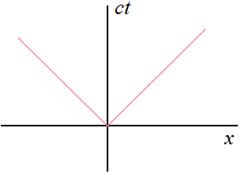
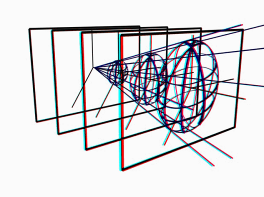
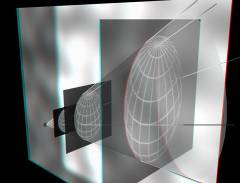
Рис. 11. Варианты изображения светового конуса в четырехмерном пространстве-времени: 1 – традиционно используемая при чтении лекций стандартная проекция на двумерную плоскость; 2, 3 – варианты выполненных анаглифическим методом демонстраций проекций четырехмерного конуса на «трехмерную евклидову плоскость»; 4 – кадр из стерео клипа, посвященного структуре пространства Минковского.

Псевдоевклидовость метрики пространства Минковского проявляется при его четырехмерных поворотах, соответствующих переходам в движущиеся (относительно исходной) инерциальные системы отсчета. Соответствующие стереоскопические видеоклипы совместно с иллюстрациями четырехмерных образов расширяющейся Вселенной для открытой и закрытой моделей, а так же – демонстрации связи между эффектами гравитационного взаимодействия и изменением геометрических свойств пространства-времени в окрестностях гравитирующих тел находятся в стадии разработки. Так же признано целесообразным создание стереоскопического учебного видеоклипа, посвященного «стереометрии четырехмерного пространства-времени». С точки зрения организации стереоскопических 3D – визуализаций основной интерес представляют демонстрации четырехмерных поверхностей, соответствующих релятивистским инвариантам типа квадратов четырехвекторов ( c2 t2 - x2 – y2 – z2 = const ).

Материалы по педагогике:

В.П. Васильев – представитель казанской школы Востоковедения
В.П. Васильев всю свою жизнь посвятил изучению Китая. Огромное количество работ В.П. Васильева по буддологии, по истории и географии Китая и сопредельных с ним стран, китайской и маньчжурской филологии по сей день привлекают внимание многих исследователей. В 1856 году З.И. Горбачев, Н.А. Петров, Г. ...

Психологические особенности развития детей шести лет
Многочисленные исследования ученых, физиологов, психологов, педагогов, практический опыт ученых-новаторов позволили прийти к выводу о возможности и необходимости обучения детей с шести лет. Это возраст, с которого целесообразно начинать систематическое обучение. Познавательная сфера шестилетних дет ...

Задания на воспитания звуковой культуры речи дошкольников
Рассмотрим эти задания и упражнения: - чередование хоровых ответов детей с индивидуальными (малыши предупреждают зайчонка об опасности; утешают, баюкают куклу и т. п.; при этом они должны быть убеждены в необходимости того, что делают). Индивидуальных и хоровых ответов должно быть достаточно много. ...

Разделы

• Главная
• Развитие познавательных интересов на уроках
• Образование как ценность
• Информатизация образования
• Образование как система и процесс
• Методологические основы педагогики
• Нравственно-этическое воспитание детей
• Образование: теория и практика
• Карта сайта
• Контакты