Образование: теория и практика » Проектирование уроков по теме "Площади плоских фигур" » Методические рекомендации к изучению темы

Методические рекомендации к изучению темы

Страница 2

4. Докажите, что два прямоугольника равны, если равны их смежные стороны.

5. На рисунке ABCD — квадрат, MN || AB, EF || BC. Найдите площадь четырехугольника AFKM, если AM=CE=3 см, DE = 6 см.

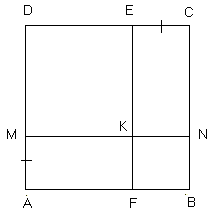
Рис. 4.

При доказательстве теоремы о площади прямоугольника желательно иметь заранее заготовленный чертеж (см. рис. 181 учебника).

В конце второго урока полезно провести самостоятельную работу обучающего характера.

Назначение параграфа — опираясь на основные свойства площадей и теорему о площади прямоугольника, вывести формулы для вычисления площадей параллелограмма, треугольника и трапеции. Кроме того, рассмотреть теорему об отношении площадей треугольников, имеющих по равному углу, на которой основано доказательство ряда теорем из последующих разделов курса.

Материал этого параграфа можно распределить по урокам следующим

образом: площадь параллелограмма — 1 урок, площадь треугольника — 2 урока, площадь трапеции — 1 урок. Оставшиеся два урока рекомендуется посвятить решению задач.

Перед выводом формулы площади параллелограмма полезно провести подготовительную работу, с тем, чтобы напомнить основные свойства площадей и признаки равенства прямоугольных треугольников:

1. На рисунке 182 учебника отрезки ВН и СК — высоты параллелограмма ABCD. Найдите площадь этого параллелограмма, если АВ = 6 см, ВС = 8 см, BAH= 30°.

В конце урока или в начале следующего урока желательно провести самостоятельную работу обучающего характера.

Перед изучением теоремы о площади треугольника полезно устно по заготовленному заранее чертежу решить следующую задачу:

2. Смежные стороны параллелограмма ABCD, равные 8 см и 12 см, образуют угол в 30°. Найдите площади треугольников ABC и ABD.

В процессе решения этой задачи повторяются основные свойства площадей, формула площади параллелограмма, акцентируется внимание на том, что диагональ делит параллелограмм на два равных треугольника.

Доказательство теоремы о площади треугольника и следствий из нее можно предложить учащимся провести самостоятельно (без учебника или с помощью него).

В основе доказательства теоремы об отношении площадей треугольников, имеющих по равному углу, лежит следствие 2° из теоремы о площади треугольника. Поэтому именно на этом следствии желательно акцентировать

внимание учащихся в процессе проверки домашнего задания (задача 474) и в процессе устного решения следующих задач:

3. На рисунке СМ — медиана треугольника AВС, СК — медиана треугольника АСМ. Найдите отношение площадей .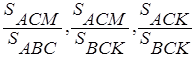

Рис. 5.

4. На рисунке точка М — середина стороны АВ, К — середина стороны СD выпуклого четырехугольника ABCD. Докажите, что SMBKD = SABCD

Доказательство теоремы об отношении площадей треугольников, имеющих по равному углу, рекомендуется провести самому учителю.

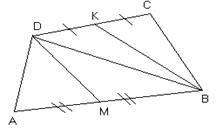
Рис. 6.

На применение теоремы об отношении площадей треугольников в классе можно решить следующую задачу (устно).

5. На рисунке 7 A=K, AC = 5 см, АВ = 3 см, KN = 7 см, KM = 2 см. Найдите отношение .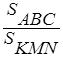

6. На рисунке 8 ОА=8 см, ОВ = 6 см, ОС = 5 см, OD = 2 см, SAOB = 20 см2. Найдите SCOD .

Рис. 7.

Рис. 8.

7. Площадь одного равностороннего треугольника в три раза больше, чем площадь другого равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1.

8. Задача 479 (б).

Доказательство теоремы о площади трапеции можно предложить учащимся разобрать дома самостоятельно.

В конце урока можно провести самостоятельную работу обучающего характера.

Назначение этих уроков – закрепить навыки в решении задач по теме «Площадь» и подготовиться к контрольной работе. Материал к этим урокам подбирается из нерешенных задач к §1 – 3, а также из дополнительных задач к главе VI.

Задачу 489 желательно решить на первом из этих уроков (вывод формулы площади равностороннего треугольника). На втором уроке следует провести самостоятельную итоговую работу.

Доказательство формулы о площади правильного многоугольника можно предложить учащимся разобрать дома самостоятельно.

Страницы: 1 2 3

Материалы по педагогике:

Применение интеллектуальных систем для анализа данных
Гибридные экспертные системы – это такой метод решения неформализованных задач, с использованием которого задачу можно представить в виде иерархического дерева подзадач и указать для каждой из них свой метод решения. За основу работы гибридных экспертных систем положена гибридная модель представлен ...

Единая образовательная информационная среда университета
Внедрение быстро развивающихся информационных технологий создало предпосылки для качественно нового этапа развития вузов на основе формирования единой образовательной информационной среды. Ее создание и развитие представляет технически сложную и дорогостоящую задачу. Но именно она позволяет системе ...

Воспитательное значение игрушек в жизни ребёнка
Актуальность изучения игры и её роли в психическом развитии ребёнка дошкольного возраста определяется особенностями игровой деятельности современных детей, значимыми для разработки адекватной стратегии психологического сопровождения развития ребёнка – дошкольника средствами игры, как ведущей для да ...

Методические рекомендации к изучению темы

Разделы