Классификация ошибок по их психологической природе
Другое дело, если мы проводим отдельно для каждого множества, объединение которых дает весь класс, какое-либо построение, нахождение (скажем, корней уравнения) или доказательство. Пересечение множеств при этом может быть и не пустым, на результат это не влияет. Главное, чтобы каждый из объектов принадлежал хотя бы одному из рассматриваемых множеств. В противном случае решение будет неполным. Приведем пример:
Пример А3: Все треугольники равновелики.
Решение: Пусть стороны треугольника D равны a, b, c, соответствующие высоты ha, hb, hc, площадь равна S.
Для обозначения треугольников 
будем использовать те же обозначения только с соответствующим числом штрихов.
Так как S = ah/2, то:
|
|
(1) |
|
|
(2) |
; 
. Из (1) и (2) следует:
|
|
|
; 
. Следовательно,
,
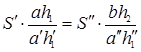или:
|
|
(3) |
. Умножив обе части равенства (3) на 
и раскрыв скобки, получим:
|
|
(4) |
. Прибавив к обеим частям равенства (4) разность 
, получим:
|
|
(5) |
. Из (5) следует, что
|
|
(6) |
Анализ ошибки: В данном случае переход от (5) к (6) не равносильный, так как равенство (5) выполняется в двух случаях:
1) 
, тогда не обязательно, чтобы 
.
2) 
, тогда обязательно .
Заметим, что всегда. Поэтому, отбросив первый случай, ученик по сути дела пошел по неверному пути. Все ученики хорошо знают, что на ноль делить нельзя. Тем не менее они часто делят на выражения без проверки равенства последних нулю.
Приведем еще один пример, когда рассмотрены не все возможные случаи.
Пример А4: Дан треугольник ABC. Проведена высота BH, равная 4. Найдите площадь треугольника ABC, если известно, что AH=6, BC=5.
Решение: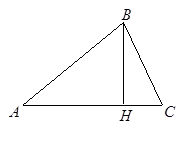 
Так как треугольник BCH прямоугольный, то
CH = 
= 3.
Значит AC = AH + HC = 6 + 3 = 9.
Площадь треугольника ABC соответственно равна:
.
Анализ решения: В рассуждениях ошибок нет, но не рассмотрен случай, когда треугольник ABC – тупоугольный. Рассуждения будут аналогичными, а ответ другой. Очевидно, ученик бессознательно использовал в решении особенности своего чертежа, не вытекающие из условия задачи.
Материалы по педагогике:
Наглядность как одно из универсальных средств обучения
иностранному языку, ее формы, достоинства и недостатки
Сочетание слова и наглядности – это одно из самых распространенных явлений в современной практике обучения. Задачи обучения решаются успешнее в том случае, когда использование языка опирается на непосредственное восприятие обучающимися предметов, процессов и их изображений. При сочетании словесного ...
Трудовое обучение младших школьников в коррекционной школе VIII вида
Ещё полвека назад В.А. Сухомлинский писал: « Детское сердце чутко к призыву творить красоту… важно только, чтобы за призывом следовал труд.». Включение детей с отклонениями в интеллектуальном развитии в трудовую деятельность с самого начала развития олигофренопедагогики признавалось одним из главны ...
Виды уроков профессионального обучения, их характеристика
В педагогике существует большое количество различных современных уроков. Можно выделить следующие группы таких уроков: 1. Уроки в форме соревнований и игр: конкурс, турнир, эстафета, дуэль, КВН, деловая игра, ролевая игра, кроссворд, викторина. 2. Уроки, основанные на формах, жанрах и методах работ ...
Разделы
- Главная
- Развитие познавательных интересов на уроках
- Образование как ценность
- Информатизация образования
- Образование как система и процесс
- Методологические основы педагогики
- Нравственно-этическое воспитание детей
- Образование: теория и практика
- Карта сайта
- Контакты
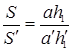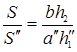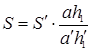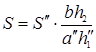