Образование: теория и практика » Анализ ошибок заочной математической школы » Классификация ошибок по их психологической природе

Классификация ошибок по их психологической природе

Страница 1

В процессе мыслительной деятельности ученик познает новые объекты и связи между ними с помощью особых умственных операций. Основными мыслительными операциями являются анализ, синтез, сравнение, абстракция, конкретизация и обобщение. Эти операции составляют различные взаимосвязанные, переходящие друг в друга стороны мышления, поэтому четкого разделения ошибок на классы сделать невозможно. Тем не менее, можно выделить ошибки, которые могут возникнуть при определенном типе мыслительного процесса.

Анализ – это мысленное разложение целого на части или мысленное выделение из целого его сторон, действий, отношений. Анализ применяется при изучении понятий, предложений и при доказательстве утверждений.

Одним из видов анализа является следующая процедура: разложение множества рассматриваемых объектов A на несколько подмножеств B1, B2, …,Bn ("случаев") по какому-то определенному критерию и работа с каждым из них отдельно. При этом должны выполнятся следующие условия: 1) объединение всех подмножеств должно совпадать с самим множеством ; 2) пересечение любых двух подмножеств пусто Впрочем, выполнение второго свойства необходимо лишь в задачах на подсчет объектов. В задачах на доказательство это условие необязательно.

Исходя из вышесказанного, при решении задач методом разложения класса на подмножества могут возникнуть ошибки двух видов:

1) существуют объекты, которые не были рассмотрены: (неполный перебор).

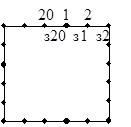Задача А1: В математическом кружке занимается 20 учеников. Им задали на дом 20 задач. Оказалось, что каждый член кружка решил ровно 2 задачи, и каждая задача решена ровно двумя учениками. Докажите, что руководитель кружка сможет так организовать разбор всех задач, что каждый ученик расскажет решение задачи, которую он сам решил. Если сможет, то сколькими способами?

Решение: Начертим граф, в котором вершины – ученики, ребра – задачи. Если две вершины (ученика) соединены ребром (задачей), значит ученики решили одну и ту же задачу. От каждой вершины отходит ровно два ребра, так как каждый решил ровно две задачи. Если этот граф развернуть, то получится замкнутый контур (см. рисунок). Наглядно понятно, что существует два способа распределения задач. Они строятся следующим образом. Первый: ученик «1» рассказывает задачу «з1», ученику «2» остается рассказать лишь задачу «з2», ученику «3» - «з3» и так далее, ученик «20» рассказывает задачу «з20». Второй: ученик «1» рассказывает задачу «з20», ученик «20» - «з19», …, ученик «2» - рассказывает задачу «з1». Получается, что преподаватель сможет организовать разбор задач двумя способами.

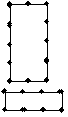
Анализ ошибки. Не рассмотрен случай, когда граф состоит из нескольких замкнутых частей, например такой граф (см. рисунок). В этом случае разбор может быть осуществлен 2n способами, где n – количество контуров. Причина в том, что при составлении цепочки от какого-то ученика школьник не рассматривает случай ее замыкания раньше, чем на 20 звене. Таким образом, ученик произвел неполный перебор: не рассмотрел случай несвязного графа.

2) в разложении существует два подмножества Bi и Bk такие, что .

Рассмотрим задачи, в которых требуется сосчитать количество объектов, удовлетворяющих данному условию.

Задача А2: Сколько существует положительных чисел, меньших 100, которые делятся на 2 или на 3.

Решение: Чисел, делящихся на 2 – 49. Чисел, делящихся на 3 – 33. Чисел, делящихся на 2 или на 3: 49 + 33 = 82.

Ответ: 82.

Анализ ошибки: При решении данной задачи не было учтено существование чисел, которые делятся на 6 (на 2 и на 3). В результате такие числа были подсчитаны два раза: первый – как делящиеся на 2, второй – как делящиеся на 3.

При решении такого рода задач (задач на подсчет количества элементов, удовлетворяющих условию задачи), следует разделять множество всех объектов на попарно непересекающиеся множества или каким-то образом учитывать их пересечения.

Страницы: 1 2 3

Материалы по педагогике:

Роль взрослого в формировании у дошкольников гуманных чувств
Формирование гуманного отношения к людям и природе начинается с раннего возраста. Главное направление в методике - проявлять по отношению к ребенку любовь, ласку, чаще употреблять ласковые слова, поглаживание, хвалить малыша за каждое проявление доброжелательности к людям (улыбнулся, отдал игрушку) ...

Постановка оперативных целей обучения и выбор источников информации
Если проанализировать стратегические цели, стоящие перед высшей школой, – всестороннее развитие личности, гарантирующее готовность к профессиональной деятельности –, то реализация этих целей возможна лишь на пути усвоения студентами суммы знаний, умений и навыков, определенных учебными программами. ...

Психолого-педагогические особенности младших школьников с особыми образовательными потребностями
Основная идея всей современной педагогики заключается в том, что отсталому ребёнку воспитание нужно в большей степени, чем нормальному. Выясним, что собой представляют дети с особыми образовательными потребностями и какие особенности психики данных детей необходимо учитывать в их воспитании и обуче ...

Классификация ошибок по их психологической природе

Разделы