Образование: теория и практика » Формирование умения обобщать у младших школьников при изучении математики » Проект по развитию умения обобщать младших школьников при изучении математики

Проект по развитию умения обобщать младших школьников при изучении математики

Страница 3

900:75= 75·12=

900:12= 75·11=

В решении этого упражнения можно вызвать одного ученика к доске, остальные ученики слушают и фиксируют в тетрадях.

Ученик решает пример в столбик:

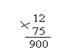
После вычисления учитель просит сравнить данный пример с остальными в этом столбике. Если школьник затрудняется с ответом, учитель может задавать наводящие вопросы, например: «Посмотри, что общего в примере, который ты решил, и в остальных; чем похожи, что в них одинаково». Ученик должен заметить, что произведение 1-ого примера равно делимому 2-ого и 3-его, делитель соответственно равны множителям 1-ого примера. Соответственно, когда школьник уловит эту взаимосвязь, он поймет, что остальные примеры вычислять не нужно, частное этих примеров есть множества 1 примера.

Переходим ко 2 столбику примеров. Учитель задает вопрос: «Чем похожи этот 1 пример и пример, который ты решил?» Ученик должен увидеть, что в обоих примерах одинаковый множитель 75.

Учитель: «А чем отличаются 2 этих примера?»

Возможный ответ ученика: «Вторым множителем и переменой места множителя 75».

Учитель: «Чем отличаются множитель в 1-м примере 12 и во 2-м примере 13?»

Ученик: «Множитель во 2 примере больше на единицу, чем в первом».

Учитель: «Правильно. Что значит 75·12? Можно ли представить произведение как сумму?

Ученик должен догадаться, что т.к. 13 больше 12 на единицу, то можно не производить умножение, а к полученному результату первого примера прибавить 75. Аналогично решаются 2 других примера.

На данном этапе трудности, которые могут подождать младшего школьника, заключаются в том, что вначале в сравнении учащиеся легко выделяют различия и труднее – сходство. Далее постепенно они выделяют и сравнивают сходство, причем вначале яркие признаки, в том числе и существенные.

В конце этапа рекомендуется провести контроль над знаниями учащихся. Предполагается создать индивидуальные карточки. Проверка будет осуществляться обменом вариантов между учениками, т.о. у школьника двойной контроль: ему надо решить собственные задания и задание соседа.

Показателем сформированности приема сравнения является умение детей самостоятельно использовать его для решения различных задач, без указаний: «сравни…, укажи признаки …, в чем сходство и различие…».

Приводим конкретные примеры таких заданий:

· убери лишнее… (при выполнении его школьники ориентируются на сходство и различие признаков):

45+12>37; 230-12<224; 45+12=57

· В какой строчке записано уравнение?

А) 46 – 20 = 26 Б) в : 7 = 2 В) 16 + а > 30 Г) к ? m = n

· сумма чисел в первом столбике равна 74. Как, не выполняя сложения во втором и третьем столбиках, найти суммы чисел:

212223

303132

111213

121314

· Продолжи ряды чисел: 2, 4, 6, 8, …; 1, 5, 9, 13 …(Основа установления закономерности (правила) записи чисел – также операция сравнения).

Страницы: 1 2 3

Материалы по педагогике:

Сравнение и аналогия
Сравнение – это установление сходства или различия между предметами или их отдельными признаками . Сравнение приводит к правильному выводу, если выполняются следующие условия: сравниваемые понятия однородны и сравнение осуществляется по таким признакам, которые имеют существенное значение. Процесс ...

Методика системного анализа и оценки эффективности проведения урока физической культуры
Последовательность определения итоговой оценки 1. Оценки отдельных составляющих в каждом из восьми разделов выставляются по 5-балльной шкале. 2. Сумма оценок, деленная на число учитываемых показателей в разделе, определяет общую оценку за раздел. Оценка за восьмой раздел умножается на 2. 3. Сумма о ...

Стратегии и принципы педагогической поддержки учащихся в состоянии депривации
На сегодняшний день доказано, что в любом образовательном учреждении существует некоторый набор факторов, которые приводят к депривации. Сегодня существует возможность обучать детей в разных специализированных школах, данная возможность зависит от финансовой состоятельности родителей. Однако данная ...

Проект по развитию умения обобщать младших школьников при изучении математики

Разделы