Образование: теория и практика » Анализ ошибок заочной математической школы » Абстракция, конкретизация и обобщение

Абстракция, конкретизация и обобщение

Страница 2

Решения, в которых доказательство свойства для всего класса необоснованно заменяется проверкой лишь для одного или нескольких конкретных объектов этого класса, вообще встречаются в работах школьников достаточно часто. Рассмотрим еще один пример.

Задача О3: Докажите, что сумма любых десяти подряд идущих нечётных чисел делится на 20.

Решение: 1 + 3 + 5 + 7 + … + 19 = 100, делится на 20. Остальные суммы тоже делятся на 20.

Анализ решения: Из того, что свойство выполняется для одной последовательности чисел, еще не следует выполнение свойства для любой другой последовательности. Например, почему 1333 + …+ 1351 делится на 20? От ученика требуются пояснения, которые бы доказывали свойство для всех последовательностей, а не проверка свойства на конкретном примере. Поэтому и оценка решения должна вестись прежде всего на основе того, проверяет ученик свойство для частных случаев или он проводит свои рассуждения для всего класса рассматриваемых объектов. В нашем случае видно, что ученик просто подсчитал сумму, никакой предпосылки для обобщения он не выделяет.

Рассмотрим пример, когда строгого доказательства нет, но все-таки его можно считать верным.

Задача О4: Число при делении на 5 дает остаток 2. Какой может быть остаток при делении на 10?

Решение: 2 = 5×0 + 2 = 10×0 + 2, 7 = 5×1 + 2 = 10×0 + 7, 12 = 5×2 + + 2 = 10×1 +2 и так далее, при увеличении числа на 5 никаких других остатков, кроме 2 и 7 не будет.

В этом случае более строгих пояснений не требуется, так как действия с оставшимися объектами достаточно ясны.

В отличие от обобщения, при конкретизации происходит переход от общего к частному: от понятия к объекту, который этим понятием характеризуется; от теоремы к применению этой теоремы. В связи с этим возникают ошибки следующего вида: 1) неточное понимание определения; 2) неправильное применение теоремы, свойства.

Ученики могут понимать определение более узко (множество объектов, подходящих под определение, меньше действительного) или более широко (множество объектов, подходящих под определение, шире действительного).

Ученики в рассуждениях иногда используют предложения, которые к рассматриваемому объекту применять нельзя. Например:

Задача О5: Основание призмы имеет площадь S. Ее боковое ребро длиной k наклонено к основанию под углом a. Найдите объем призмы.

Решение: Объем призмы равен произведению площади основания на длину бокового ребра, поэтому V = S×k.

Анализ ошибки: В данном случае ученик воспользовался формулой вычисления объема для прямой призмы. Для наклонной призмы эта формула не верна, следовательно, применять ее нельзя. Единственный способ искоренить ошибку – показать ученику наглядно, что его рассуждения противоречивы. Для этого возьмем прямую призму. Разделим ее на две равные части так, как показано 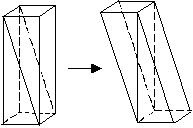на рисунке. Составим из этих частей наклонную призму. Понятно, что их объемы должны быть равны. Если же действовать подобно ученику при вычислении объемов, то объем наклонной призмы будет больше, чем объем прямой призмы.

Страницы: 1 2

Материалы по педагогике:

Метод круговой тренировки на занятиях с детьми младшего школьного возраста
Дети младшего школьного возраста обладают слабым качеством – быстрота, обладают низкими показателями мышечной силы. Дети этого возраста более расположены к кратковременным скоростно-силовым упражнениям. В этом возрасте широкое применение находят прыжковые упражнения. Например, прыжки через препятст ...

Методика проведения природоведческой беседы, виды бесед
Исходя из дидактических задач выделяют 3 вида бесед: предварительную, сопровождающую и итоговую. Предварительная беседа используется воспитателем перед наблюдением, экскурсией. Цель такой беседы — уточнение опыта детей для того, чтобы установить связь предстоящего наблюдения с имеющимися знаниями. ...

Методические рекомендации по развитию волевого поведения детей дошкольного возраста
Деятельность, которая приносит малышу удовольствие, помогает в его воспитании значительно больше, чем прямые требования исправиться, слушаться взрослых. Ниже приведены игры, направленные на развитие нравственно – волевых качеств личности. В младшем дошкольном возрасте к таким качествам можно отнест ...

Абстракция, конкретизация и обобщение

Разделы