Классификация повторения в зависимости от содержания повторяемого материала
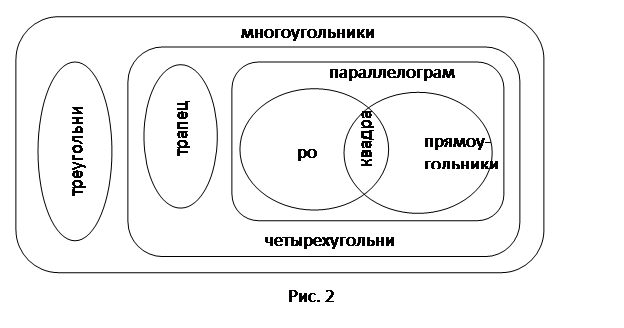При обобщающем повторении темы «Многоугольники» происходит сопоставление понятий треугольник, параллелограмм, прямоугольник, ромб, квадрат, трапеция, выясняются связи между ними. Эти понятия включаются в новые отношения, учащиеся устанавливают иерархию понятий. Результатом обобщения может служить схема, изображенная на рис. 2.
Методы работы с таблицами и схемами различны: учитель проводит беседу, выразив ее результаты в виде схемы; знакомит учащихся с планом беседы, а затем по этому плану проводит ее; знакомит учащихся со схемой, по которой они самостоятельно проводят обобщение, предлагает учащимся самостоятельно обобщить материал и выразить результаты в виде схемы.
Рассмотрев эту схему с учащимися, учитель предлагает серию вопросов:
Как определить ромб через четырехугольник, квадрат через четырехугольник, квадрат через ромб?
Можно ли определить ромб через прямоугольник?
Что является пересечением множества всех прямоугольников и множества всех ромбов?
Методика организации работы учащихся по данной теме может быть и другой. Например, учитель может лишь определить цель работы и указать основные вопросы, на которые учащиеся должны найти ответы; определить не только цель работы и перечень вопросов, но и раскрыть этапы и методику работы над этими вопросами.
При обобщающем повторении на уровне теорий дается определенная трактовка изученным понятиям с позиции тех или иных фундаментальных теорий, входящих в содержание математических курсов, при этом строится единая, общая форма многообразия частных фактов, явлений понятий. Значительное внимание уделяется происхождению понятий. Школьники устанавливают общие закономерности, причинно-следственные отношения, обобщают и конкретизируют материал, применяют общие положения к конкретным фактам. Материал, выносимый на обобщающее повторение на уровне теорий, должен представлять собой логическую систему, вопросы которой объединены той или иной фундаментальной теорией.
Обобщающее повторение на уровне теорий освещает полученные знания не только в плане внутрипредметных, но и межпредметных связей, так как многие понятия различных учебных предметов получают единую трактовку с позиций одной какой-либо теории.
Например, при повторении темы «Векторы» основное внимание следует уделить векторному методу решения задач. Сначала необходимо повторить основные теоретические факты: коллинеарность и равенство векторов, сложение, вычитание и умножение вектора на число. Основное время урока следует отвести для решения задач, показывающих применение векторов при доказательстве и решении задач.
Повторение можно организовать в ходе решения задач:
На стороне BC треугольника 
отмечена точка N так, что 
. Выразите вектор 
через векторы 
и 
.
Три точки A, B и C расположены так, что 
. Докажите, что для любой точки O справедливо равенство 
.
Доказать для того, чтобы C было серединой отрезка AB необходимо и достаточно выполнение векторного равенства 
.
Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям и равен полуразности оснований.
Докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырехугольника, точкой пересечения делятся пополам.
Материалы по педагогике:
Рисование «Украсим рукавичку домик»
Учить детей рисовать по мотивам сказки «Рукавичка», создавать сказочный образ. Развивать воображение, творчество. Формировать умение украшать предмет. Закреплять умения использовать в процессе рисования краски разных цветов; чисто промывать кисть и осушать ее о салфеточку, прежде чем взять другую к ...
Историография
Поставленная в настоящей работе проблема изучена в отечественной историографии недостаточно. Это связано с тем, что реформы высшей школы Франции в рамках Болонского процесса в настоящее время только разворачиваются, и они еще не успели стать объектом внимания исследователей. Собственно говоря, вним ...
Мастерские и кружки по интересам
Опираясь на идею воспитания русского национального духовного характера, понимая её актуальность, школа на первое место ставит задачу сбережения духовного, физического здоровья детей – будущего нации. В схеме воспитания национального духовного характера особое место занимает дополнительное образован ...
Разделы
- Главная
- Развитие познавательных интересов на уроках
- Образование как ценность
- Информатизация образования
- Образование как система и процесс
- Методологические основы педагогики
- Нравственно-этическое воспитание детей
- Образование: теория и практика
- Карта сайта
- Контакты